Schwarzkörperstrahlung: Das Plancksche Strahlungsgesetz
Das Plancksche Strahlungsgesetz beschreibt die Abstrahlung von Licht und anderer elektromagnetischer Strahlung von einem idealisierten planckschen Strahler. Da dieser Körper gleichzeitig die Eigenschaft hat, alles Licht zu absorbieren, das auf ihn fällt, wird er auch schwarzer Strahler oder schwarzer Körper genannt.
Das Plancksche Strahlungsgesetz geht dabei von fundamentalen physikalischen Zusammenhängen aus. Reale Körper (leuchtende Quecksilberatome, Glühwendeln, glühende Rußpartikel …) werden immer weniger Licht abstrahlen als ein planckscher Strahler.
Pro Raumwinkel strahlt ein planckscher Strahler die spektrale Strahldichte $L_\lambda(\lambda,T)$ ab, die von der Wellenlänge $\lambda$ und der Temperatur $T$ abhängt: \[ L_\lambda(\lambda,T)= \frac{\partial L(\lambda,T)}{\partial \lambda)} = \frac{2hc^2}{n^2\lambda^5} \frac{1}{\mathrm{e}^{\frac{hc}{k_Bn\lambda T}}-1} \] ($k_B=1,380\times10^{-23}\text{J}/\text{K}$: Bolzmann-Konstante, $n$: Brechungsindex, $h=6,626\times 10^{-34}\text{Js}$: Planck-Konstante, $c=3\times 10^8\text{m}/\text{s}$: Lichtgeschwindigkeit)
Um daraus die Strahlungsleistung ($\Phi$) zu bestimmen, muss die Strahldichte ($L$) über den Raumwinkel, in den die Quelle abstrahlt ($\Omega$) und die Oberfläche des planckschen Körpers ($A$, wobei $\theta$ der Winkel ist, unter dem Licht aus der Fläche austritt oder auf sie trifft) integrieren. Der plancksche Strahler strahlt dabei Licht gleichmäßig in den vollen Raumwinkel von $4\pi$ aus. \[ \Phi_\lambda = \int d\Omega \int d A \cos(\theta) \,\, L_\lambda(\lambda,T) = \int\limits_0^{\pi} d \theta \int\limits_0^{2\pi} d\phi \, \sin(\theta) \, \int d A \cos(\theta) \,\, L_\lambda(\lambda,T) = 4\pi \, A \, L_\lambda(\lambda,T) \] \[ \Phi_\lambda(\lambda,T) = \frac{8{\pi}hc^2}{n^2\lambda^5} \frac{A}{\mathrm{e}^{\frac{hc}{k_Bn\lambda T}}-1} \]
Ich stelle hier einen Excel-Rechner zur Verfügung, mit der das Spektrum eines Schwarzen Strahlers berechnet werden kann.
maximale Lichtausbeute eines Schwarzkörperstrahlers
Das plancksche Strahlungsgesetz gibt zunächst eine maximale Strahlungsleistung $\Phi$, die eine eine Lichtquelle mit einer Oberfläche $A$ und einer Temperatur $T$ bei einer Wellenlänge $\lambda$ abstrahlen kann. Bei realen Lichtquellen liegt diese Strahlungsleistung normalerweise um viele Größenordnungen geringer, vor allem für die meisten Wellenlängebereiche und Temperaturen.
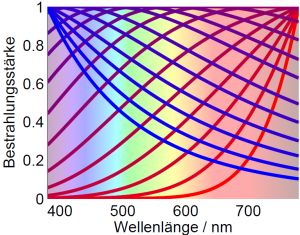
Eine Glühbirne mit einem Glühdraht von $L=1\text{m}$ Länge und $D = 0.02 \text{mm}$ Durchmesser könnte daher bei $T=2800 \text{K}$ maximal folgende Strahlungleistung abstrahlen: \[ \Phi_\lambda(\lambda) = \frac{8{\pi}hc^2}{\lambda^5} \frac{LD\pi}{\mathrm{e}^{\frac{hc}{k_Bn\lambda T}}-1} = \frac{9.42\times 10^{-20}\text{W}\text{m}^4}{\lambda^5}\frac{1}{\mathrm{e}^{\frac{hc}{k_Bn\lambda T}}-1} \] Verteilt man die Strahlungsleistung (linke Achse) noch auf eine Kugelfläche mit 30 cm Radius so erhält man die Bestrahlungsstärke (rechte Achse), die ein Spektrometer in 30cm Abstand messen würde. Wolfram erreicht das theoretische Maximum eines Planckschen Strahlers nicht (blaue Linie). Der Emissionskoeffizient liegt nur bei etwa 0.3. Das so berechnete Spektrum stimmt sehr gut mit dem tatsächlich gemessenen Spektrum eines 50W Halogenspots überein. Eine 100 W Lampe, die entsprechend doppelt so viel Licht abstrahlen soll müsste einen Glühdraht enthalten, der die doppelte Oberlfäche hat.
Ein theoretischer (und aus thermodynamischen Gründen unerreichbarer) Maximalwert der Lichtausbeute bestünde, wenn sämtliche aufgenommene elektrische Energie vollständig in Strahlungsleistung umgesetzt würde. Hat diese Strahlungsleistung die spektrale Verteilung eines Schwarzen Strahlers, strahlt aber nur im sichtbaren Bereich (400nm-800nm) ab so gilt:
\[ \eta = \frac{\Phi_\mathrm{vis}}{\Phi_\mathrm{energ.}} = 683\frac{\mathrm{lm}}{\mathrm{W}} \frac{ \int\limits_{400}^{800}\mathrm{d}\lambda V(\lambda)\frac{1}{\lambda^5\mathrm{e}^{\frac{0.014388\mathrm{mK}}{\lambda T}}-1} }{ \int\limits_{400}^{800}\mathrm{d}\lambda \frac{1}{\lambda^5\mathrm{e}^{\frac{0.014388\mathrm{mK}}{\lambda T}}-1} } \]
| Temperatur $T$ | Effizienz $\eta$ |
|---|---|
| 2000K | 86 lm/W |
| 3000K | 157 lm/W |
| 4000K | 193 lm/W |
| 5000K | 207 lm/W |
| 5500K | 210 lm/W |
| 6000K | 211 lm/W |
| 6500K | 212 lm/W |
| 7000K | 212 lm/W |
| 8000K | 211 lm/W |
| 9000K | 209 lm/W |
| 15000K | 200 lm/W |
Discussion