Table of Contents
Wichtige Einheiten
Elektromagnetische Strahlung besteht physikalisch aus einem Strom quantenmechanischer Teilchen, sogenannter Photonen, kann aber in vielen Fällen auch klassisch als elektromagnetische Welle beschrieben werden. Manchmal lässt sich das Verhalten der Strahlung besser im klassischen Wellenbild beschreiben (z.B. bei der Ausbreitung von Licht in engen Strukturen), manchmal besser im Teilchenbild (z.B. bei der Wechselwirkung mit biologischen Systemen).
Im klassischen Wellenbild nimmt ein elektrisches Feld in seiner Stärke zeitlich wellenförmig zu und ab, breitet sich dabei wie eine Welle im Raum aus und wird von einem magnetischen Feld begleitet. Die Ausbreitungsgeschwindigkeit im Vakuum ist eine physikalische Konstante, die Lichtgeschwindigkeit c = 3×108 m/s. Über diese Geschwindigkeit hängen die räumliche Wellenschwingung mit Wellenlänge $\lambda$ und räumlicher Frequenz bzw. Wellenzahl $k$ und die zeitliche Wellenschwingung mit zeitlicher Frequenz $f$ und Kreisfrequenz $\omega$ zusammen ($\lambda f = c = \frac{\omega}{k}$). Die Strahlungsmenge wird im klassischen Wellenbild als Energiemenge (Watt, Joule) gemessen.
| Größe | Wellenlänge | Wellenzahl | Kreiswellenzahl | Periode | Frequenz | Kreisfrequenz |
|---|---|---|---|---|---|---|
| Formelzeichen | $\lambda$ | $k = {1} / \lambda $ | $k = {2 \pi} / \lambda $ | $T = \frac{\lambda}{c}$ | $f = 1/T$ oder $\nu$ | $\omega = {2 \pi} / T$ |
| Bedeutung | Länge der räumlichen Schwingung | Ortsfrequenz der räumlichen Schwingung | Ortsfrequenz der räumlichen Schwingung | Dauer der zeitlichen Schwingung | Frequenz der zeitlichen Schwingung | Kreisfrequenz der zeitlichen Schwingung |
| Einheit | m | cm-1 | cm-1 | fs | THz | THz |
| Beispiel | 500 nm | 20'000 cm-1 | 1,26×105 cm-1 | 1,67 fs | 600 THz | 3800 THz |
Im quantenmechanischen Teilchenbild bewegen sich Photonen mit einer festen Energie mit Lichtgeschwindigkeit fort. Obwohl Photonen keine Masse haben, haben sie dennoch einen Impuls, was in der klassischen Welt nur bei Teilchen mit Masse möglich ist. Da Teilchen zählbar sind, kann die Gesamte Menge elektromagnetischer Strahlung nicht nur als Gesamtenergie gemessen werden, sondern auch als Photonenzahl angegeben werden, meist als Vielfaches der Menge Mol (6,022×1023 Teilchen). Elementare Konstante der Quantenwelt ist das Plancksche Wirkungsquantum h = 6,626×10-34Js = 4,136×10-15eVs
| Größe | Energie | Impuls |
|---|---|---|
| Formelzeichen | $E = h\cdot{}f = h\cdot{}c/\lambda $ | $p = h/\lambda = h\cdot{}f/c $ |
| Bedeutung | Energie eines Photons | Impuls eines Photons |
| Einheit | J oder eV | Ns oder kg/m/s² |
| Beispiel | 2.48 eV = 3.97×10-19 J | 1.33×10-27 Ns |
Sonnenspektrum in verschiedenen Einheiten
Die unterschiedlichen Einheiten für Strahlungsmengen (Gesamtenergie, Gesamtimpuls, gesamte Teilchenzahl) und für die verschiedenen Strahlungsbereiche (Energie eines Photons, Impuls eines Photons, Wellenlänge, Wellenzahl, Frequenz, Periode) sind besonders dann wichtig, wenn ein Spektrum der Strahlung dargestellt werden soll. In einem Spektrum wird aufgezeichnet, welche Menge in welchem Bereich vorhanden ist. Je nach dem welche Einheiten gewählt werden, sieht das Spektrum sehr unterschiedlich aus.
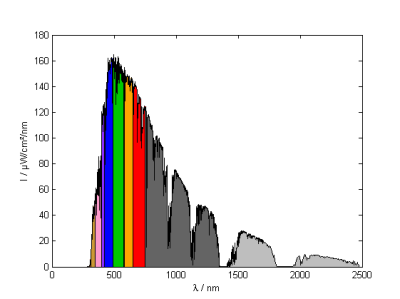
(1) W/cm²/nm : Energy pro Wellenlänge
In der Beleuchtungstechnik verwendet man meist die Einheit W/m²/nm oder µW/cm²/nm (1 W/m²/nm = 100 µW/cm²/nm): welche Leistung (Energie pro Zeit) kommt auf einer bestimmten Fläche innerhalb eines Wellenlängenbereichs an.
Geplottet wird $\left(\lambda ; \frac{dE}{d\lambda}\right)$ mit den Einheiten [nm;µW/cm²/nm]
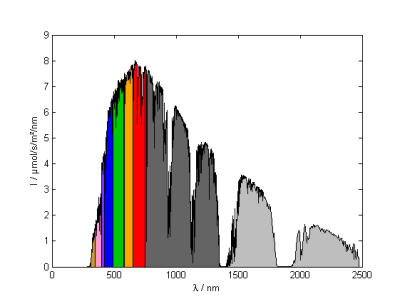
(2) nmol/s/m²/nm : Photonenzahl pro Wellenlänge
In der Biologie und der Chemie wählt man meist die Einheit mol/s/m²/nm: welche Photonenzahl kommt auf innerhalb einer bestimmten Zeit, einer bestimmten Fläche und innerhalb eines Wellenlängenbereichs an. 1 Photon hat die Energie hc/λ - der Wert ist verschwindet gering, so dass man üblicherweise die Energie von 1 mol (also 6.02214076×1023 Stück) Photonen zusammen fasst. Da Photonen mit kurzer Wellenlänge mehr Energie tragen, wirkt das Spektrum in dieser Einheit rotlastig.
Geplottet wird $\left(\lambda ; \frac{dN}{d\lambda}\right)$ mit Einheiten [nm;mol/s/m²/nm].
- $\frac{dN}{d\lambda} = \frac{dE / \left(h\cdot\frac{c}{\lambda}\right)}{d\lambda} = \frac{dE}{d\lambda} \cdot \frac{\lambda}{h\cdot c}$
- 100 µW/cm²/nm bei 500 nm entsrechen: $ 100 µW/cm²/nm \cdot \frac{500 nm}{6.626\times{}10^{-34}Js\cdot{}3\times{}10^{8}m/s} \\ = 100\times{}10^{-6} J/s/cm²/nm \cdot \frac{500 \times{}10^{-9}m}{6.626\times{}10^{-34}Js\cdot{}3\times{}10^{8}m/s} \\ = \frac{5}{6.626\cdot{}3}\times{}10^{2-6+2-9+34-8} \cdot \frac{J \cdot{}m\cdot{}s}{s\cdot{}cm²\cdot{}nm\cdot{}J\cdot{}s\cdot{}m} \\ = \frac{5}{6.626\cdot{}3}\times{}10^{15} \cdot \frac{1}{s\cdot{}cm²\cdot{}nm} \\ = \frac{5}{6.626\cdot{}3\cdot{}6.022}\times{}10^{-8} \cdot \frac{mol}{s\cdot{}cm²\cdot{}nm}$
= 0,4 nmol/s/cm²/nm
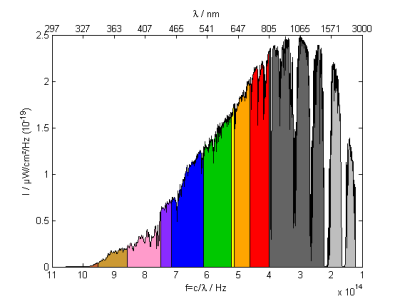
(3) W/cm²/Hz : Energie pro Frequenz bzw. Energie pro Photonenenergie
In den beiden ersten Fällen wurde die Strahlungsbereich anhand der Wellenlänge unterschieden. Diese Einteilung ist bei Gitterspektrometern natürlich. Es gibt jedoch auch die Darstellung in Abhängigkeit der Frequenz. Prismen zerlegen das Licht näherungsweise in gleiche Frequenzbereiche. Bei der Darstellung als Funktion der Frequenz wird der rote Spektralbereich zusammengedrückt, der blaue Bereich gestreckt. Es ändert sich aber nicht nur die Abszisse (x-Achse) sondern auch die Ordinate (y-Achse). Da die einzelnen Bereiche im Roten schmaler werden, müssen sie gleichzeitig höher werden, damit die Energie oder die Teilchenzahl unverändert bleibt.
Die Frequenz auf der x-Achse ist auch direkt proportional zur Energie der einzelnen Photonen.
Geplottet wird $\left(f; \frac{dE}{df}\right)$ mit Einheiten [Hz;µW/cm²/Hz].
Rechnung:
$f = \frac{c}{\lambda}$
$\frac{dE}{df} = \frac{dE}{d\lambda} \cdot \frac{d\lambda}{df} = \frac{dE}{d\lambda} \cdot \left(\frac{df}{d\lambda}\right)^{-1} = \frac{dE}{d\lambda} \cdot \left(\frac{d c/\lambda}{d\lambda}\right)^{-1} = \frac{dE}{d\lambda} \cdot \left(\frac{c}{\lambda^2}\right)^{-1} = \frac{dE}{d\lambda} \cdot \frac{\lambda^2}{c} $.
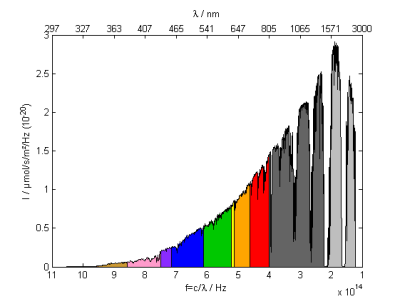
(4): mol/s/m²/Hz : Photonenzahl pro Photonenenergie
Die letzte Darstellung ist aus Sicht der Photochemie vielleicht die natürlichste. Prozesse, bei denen organische Moleküle Licht absorbieren, werden durch die Anzahl der Photonen und eher durch die Energie des einzelnen Photons als durch dessen Wellenlänge bestimmt. Hier erscheint das Sonnenspektrum extrem Infrarotlastig.
Geplottet wird $\left(f; \frac{dN}{df}\right)$ mit Einheiten [Hz;mol/s/m²/Hz].
Rechnung:
$f = \frac{c}{\lambda}$
$\frac{dN}{df} = \frac{dE}{df} \cdot \frac{\lambda}{h\cdot c} = \frac{dE}{d\lambda} \cdot \frac{\lambda^2}{c} \cdot \frac{\lambda}{h\cdot c} = \frac{dE}{d\lambda} \cdot \frac{\lambda^3}{hc^2} $.
Discussion
Habe eine Frage zur Erwärmung von Material (z.B. Kunststoff) abhängig von der Wellenlänge des Lichtes (z.B. der Sonne): * Wie ist der Zusammenhang zwischen der Wellenlänge und der Erwärmung des bestrahlten Materials. Sprich: werden Materialien auch durch das UV Licht der SOnne erwärmt oder nur durch die IR Komponente des Lichts?
Hallo, grundsätzlich kann jede Wellenlängen Material erwärmen. Es kommt auf das Material an: Wenn das Material die Wellenlänge absorbiert und nicht anderweitig nutzt, dann wird das Material warm. Sichtbares Licht erwärmt Glas nicht, weil Glas sichtbares Licht nicht absorbiert (es ist durchsichtig). Solarzellen werden von sichtbarem Licht schlechter erwärmt , weil das sichtbare Licht zwar absorbiert aber nicht in Wärme sondern in Strom umgewandelt wird.
Grundsätzlich trägt UV aber wenig zur Erwärmung bei, weil die Gesamtmenge an UV-Strahlung im Sonnenlicht sehr gering ist im vergleich zur sichtbaren Strahlung und zur Infrarotstrahlung.