Farbe aus photometrischer Sicht ist eine sehr mathematische Angelegenheit die mit den Methoden der linearen Algebra bearbeitet wird und Farbmetrik genannt wird.

Aus Physikalischer Sicht steckt die volle Information über da Licht das unsere Augen erreicht in dessen Spektrum, das angibt welche Wellenlänge mit welcher Intensität vertreten ist. Der Mensch hat drei Zapfen (nicht Zäpfchen!), L (long wavelength), M (middle wavelength) und S (short wavelength), die vom einfallenden Licht unterschiedliche gereizt werden, und so eine Unterscheidung der spektralen Zusammensetzung des Lichts ermöglichen, also eine Farbwahrnehmung ermöglichen.

L-Zapfen

M-Zapfen

S-Zapfen

Das Licht mit dem Spektrum $s(\lambda)$ reizt jeden Zapfen gemäß seiner spektralen Empfindlichkeitskurve:

\[ R_S = \int\limits_{380\mathrm{nm}}^{780\mathrm{nm}}\mathrm{d}\lambda s(\lambda) S(\lambda) ,\qquad R_M = \int\limits_{380\mathrm{nm}}^{780\mathrm{nm}}\mathrm{d}\lambda s(\lambda) M(\lambda) ,\qquad R_L = \int\limits_{380\mathrm{nm}}^{780\mathrm{nm}}\mathrm{d}\lambda s(\lambda) L(\lambda) \]

Der Farbeindruck ergibt sich aus der (relativen) Stärke der drei Reize $R_S$, $R_M$, $R_L$ der drei Zapfen, die in der Netzhaut verarbeitet und ins Gehirn weitergeleitet werden.

Die spektralen Empfindlichkeitskurven der drei Zapfen wurde erst relativ spät experimentell ermittelt. Die Berechnung von Farben ist jedoch einige Jahre älter, so dass nicht mit den Zapfenempfindlichkeiten gerechnet werden konnte. Stattdessen wird mit den Normspektralwertkurven X, Y und Z gearbeitet.

Diese Normspektralwertkurven wurden experimentell in den 1920er Jahren ermittelt:

Ein Feld wurde mit monochromatischem Licht der Wellenlängen 380nm bis 780nm in 5nm Schritten beleuchtet. Dieses Feld hat die Farbe $C_1$. Ein zweites Feld mit einer Mischung der Wellenlängen 700nm (rot), 546,1nm (grün) und 435,8nm (blau) beleuchtet. Die grüne und blaue Linie sind Linien der Quecksilberdampflampe. 700nm waren schwer zu produzieren, weswegen eine Wellenlänge gewählt wurde, bei der das menschliche Auge kleine Unterschiede nur schlecht wahrnimmt.

Für jede Wellenlänge muss ein Mensch nun das Mischverhältnis so anpassen, dass die Farbe in beiden Feldern gleich ist.

\[ C_{\lambda_1} = r(\lambda_1)C_R + g(\lambda_1)C_G + b(\lambda_1)C_B\]

Das ist nicht immer möglich, da sich nicht alle Farben aus drei Farben mischen lassen. Es ist aber immer möglich, wenn man auch zur monochromatischen Testfarbe rot, grün oder blau hinzumischen kann. Beispielsweise kann eine Farbe $C_2$ zu der man einen Teil rot mischt durch eine Mischung von blau und grün dargestellt werden:

\[ C_{\lambda_2} + r(\lambda_2)C_R = g(\lambda_2)C_G + b(\lambda_2)C_B \]

\[ C_{\lambda_2} = g(\lambda_2)C_G + b(\lambda_2)C_B - r(\lambda_2)C_R\]

Normiert man $r(\lambda), g(\lambda), b(\lambda)$ so, dass weißes Licht durch $\overline r=\overline g=\overline b$ dargestellt wird erhält man:

CIE-B

CIE-G

CIE-R

Dass diese Kurven auch negativ werden können ist unschön, man geht daher durch eine linear Transformation auf $\overline x$, $\overline y$ und $\overline z$ über, die so ausgewählt werden, dass weiß durch X=Y=Z dargestellt wird, und zusätzlich Y dem Hellempfindlichkeitsgrad des menschlichen Auges entspricht.

\[ \left( \begin{array}{c} \overline x(\lambda)\\\overline y(\lambda)\\\overline z(\lambda) \end{array} \right) = \left( \begin{array}{ccc} 2,76888&1,75175&1,13016\\1,00000&4,59070&0,06010\\0,00000&0,05651&5,59427 \end{array} \right) \left( \begin{array}{c} \overline r(\lambda)\\\overline g(\lambda)\\\overline b(\lambda) \end{array} \right)\]

CIE-X

CIE-Y

CIE-Z

Eine Farbe ist nun also rechnerisch gegeben durch den Anteil X, Y und Z

\[X = \int\limits_{380\mathrm{nm}}^{780\mathrm{nm}}\mathrm{d}\lambda \overline x(\lambda) s(\lambda) ,\qquad Y = \int\limits_{380\mathrm{nm}}^{780\mathrm{nm}}\mathrm{d}\lambda \overline y(\lambda) s(\lambda) ,\qquad Z = \int\limits_{380\mathrm{nm}}^{780\mathrm{nm}}\mathrm{d}\lambda \overline y(\lambda) s(\lambda)\]

Dieses Werte-Triplett (X,Y,Z) kann als Punkt in einem dreidimensionalen Raum dargestellt werden. Zwei Spektren die den selben Punkt ergeben, werden vom Menschen als selbe Farbe wahrgenommen.

Farborte reiner Spektralfarben

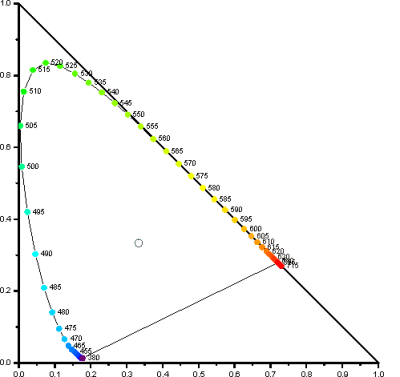
Unter der Annahme, dass die wahrgenommene Farbe nicht von der Intensität des Lichts, sondern nur vom Verhältnis der Reize auf die drei Zapfen bestimmt wird (stimmt nicht ganz), kann man von dem dreidimensionalen Farbpunkt (X,Y,Z) auf einen zweidimensionalen Farbpunkt (x,y) übergeben. Eine Möglichkeit dazu ist: x = X/(X+Y+Z) und y=Y/(X+Y+Z). Das macht es möglich, die Farbe leicht in einer zweidimensionalen Farbtafel aufzuzeichnen. Da $X(\lambda)$, $Y(\lambda)$ und $Z(\lambda)$ bekannt sind, kann man leicht $x(\lambda)$ und $y(\lambda)$ ausrechnen und die Punkte aufzeichnen. Dabei ergibt sich (zufällig - es hängt von der Definition von X,Y,Z ab) eine hufeinsenförmige Kurve.

Theoretisch sind nach der Formel x+y+z=1 alle Punkte innerhalb des Dreieckes möglich. Man kann aber leicht ausrechnen, dass die Mischung zweier Farben immer auf der Verbindungslinie zwischen den beiden Farben liegt: Addiert man zwei Farben im XYZ-Farbraum $C_1 = \left(\begin{array}{c}X_1\\Y_1\\Z_1\end{array}\right)$ und $C_2 = \left(\begin{array}{c}X_2\\Y_2\\Z_2\end{array}\right)$ so kann man die Vektoren einfach nach den Gesetzen der Vektoraddition addieren. In der xy-Farbtafel ist das nicht mehr möglich. Hier liegt die Mischfarbe von $c_1 = \left(\begin{array}{c}x_1\\y_1\end{array}\right)$ und $c_2 = \left(\begin{array}{c}x_2\\y_2\end{array}\right)$ auf der Verbindungslinie von $c_1$ und $c_2$. Je mehr $c_1$ in der Mischung vorhanden ist, desto näher liegt die neue Farbe bei $c_1$.

Physikalisch kann ein farbiges Licht nur aus reinen Wellenlängen zusammengesetzt sein, d.h. alle Farben können nur innerhalb der hufeisenförmigen Spektralfarblinie liegen, Farben außerhalb sind praktisch nicht möglich, und werden als virtuelle Farben bezeichnet.

Der Punkt an dem X=Y=Z, d.h. x=y=0,33 gilt, wird Unbuntpunkt genannt.

Da durch additive Farbmischung nur ein kleiner Anteil der reellen Farben darstellbar ist, wurde nur ein kleiner Teil des Farbdreiecks koloriert. Spektralfarben sind mit Druckfarben und am Bildschirm grundsätzlich nicht darstellbar!

Im Farbdreieck finden sich zwar alle physikalisch vorkommenden Farben, nicht jedoch alle tatsächlich wahrgenommenen Farben! Es fehlen beispielsweise braun, olivgrün, rosa … . Nach der obigen Definition von Farben entspricht braun = orange und olivgrün = gelb. Erst durch den Vergleich mit räumlich benachbarten Helligkeit und Farben im Wahrnehmungsfeld entsteht der Eindruck einer braunen oder olivgrünen Farbe.

Dass die Farbart von Braun und Orange gleich sind, oder die von Gelb und Olivgrün, kann man experimentell mit Hilfe von zwei Projektoren schön veranschaulichen: Zunächst projiziert man in einem abgedunkelten Raum Licht durch ein oranges oder gelbes Filter mit nicht zu großer Helligkeit auf eine Leinwand; die Farbempfindung ist Orange bzw. Gelb. Dann wird mit größerer Helligkeit ein weißer Ring auf die Leinwand projiziert, und sofort erscheint das Innere des Ringes braun bzw. oliv. http://www.itp.uni-hannover.de/~zawischa/ITP/fmetr.pdf

Rote Farbe

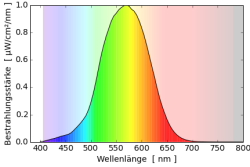
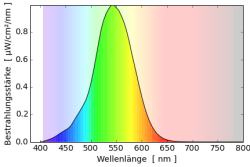
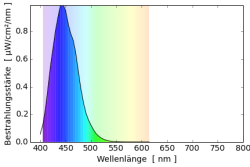
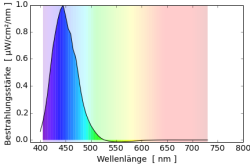
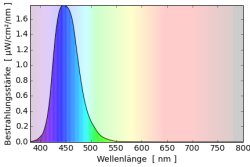
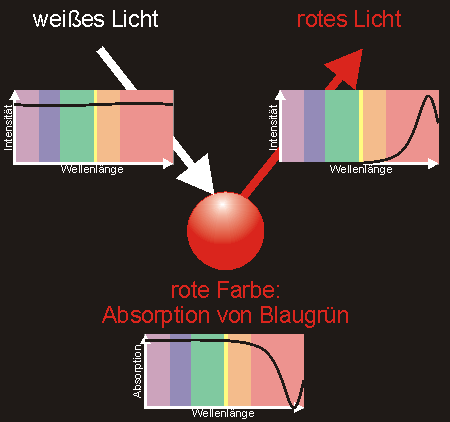
Man kann zwei Farben unterscheiden: Die Farbe von Objekten und die Farbe des Lichts das unser Auge erreicht. Zerlegt man rotes Licht in seine Wellenlängen so hat es ein große Intensität im Bereich über 600nm und wenig Intensität. Wenn man den Farbort berechnet, liegt er im Farbdreieck rechts unten. Weißes Licht dagegen bevorzugt keine Wellenlänge und die Intensität ist über alle Wellenlängen sehr gleichmäßig verteilt. Ein roter Körper muss daher alle Farben außer rot absorbieren und nur rot reflektieren, damit er aus weißem Licht rotes Licht macht, und somit rot erscheint.

“Rot” kann also zweierlei bedeuten

• rotes Licht mit viel Intensität im roten Wellenlängenbereich.
• ein rotes Objekt das im violett-blau-grün-gelben Bereich stark absorbiert und rot gut reflektiert

Bei der Mischung von zwei Farben unterscheidet man additive und subtraktive Farbmischung

• additive Farbmischung bezeichnet die Mischung von Lichtfarben
• subtraktive Farbmischung bezeichnet die Mischung von Objektfarben

Als Beispiele falle weißes Licht (Spektrum $s_0(\lambda)=1$) auf rote Farbe (Reflektionsspektrum $r_1$) bzw. auf grüne Farbe (Reflektionsspektrum $r_2$). Dabei entsteht rotes Licht $s_1=s_0r_1$ und grünes Licht $s_2=s_0r_2$. Die (additive) Mischung der beiden Lichter ergibt $s_A = s_1+s_2 = s_0(r_1+r_2)=r_1+r_2$. Die einzelnen Reflektionsspektren werden addiert um zur neuen Farbe zu gelangen. Man spricht daher von additiver Farbmischung.

Da alle benötigte Mathematik linear ist, kann man im XYZ-Farbraum die Farben $C_1 = \left(\begin{array}{c}X_1\\Y_1\\Z_1\end{array}\right)$ und $C_2 = \left(\begin{array}{c}X_2\\Y_2\\Z_2\end{array}\right)$ auch direkt nach den Gesetzen der Vektoraddition addieren. In der xy-Farbtafel ist das nicht mehr möglich. Hier liegt die Mischfarbe von $c_1 = \left(\begin{array}{c}x_1\\y_1\end{array}\right)$ und $c_2 = \left(\begin{array}{c}x_2\\y_2\end{array}\right)$ auf der Verbindungslinie von $c_1$ und $c_2$. Je mehr $c_1$ in der Mischung vorhanden ist, desto näher liegt die neue Farbe bei $c_1$.

In der Farbtafel ist leicht ersichtlich dass:

• rot + gelb = orange
• grün + rot = gelb
• grün + lila = blau
• blau + grün = blaugrün
• rot + lila = violett
• rot/orange + blau = weiß
• grün + violett = weiß

Farben, die addiert weiß ergeben, nennt man Gegenfarben.

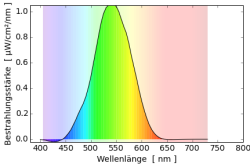
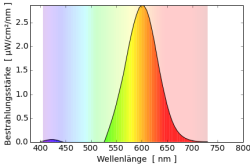
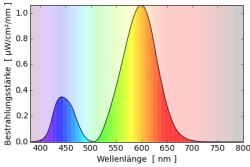
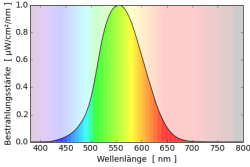
Mischt man die beiden Farbstoffe erhält man ein Reflektionsspektrum $r_S=r_1r_2$, in dem die Einzelspektren multipliziert werden. Fällt weißes Licht auf diese Farbmischung entsteht $s_S=s_0r_S=s_0r_1r_2=r_1r_2$. Die einzelnen Reflektionsspektren werden multipliziert. Der Begriff “Multiplikative Farbmischung” hat sich jedoch nicht durchgesetzt, und es wird von subtraktiven Farbmischung im Gegensatz zur additiven Farbmischung gesprochen.