Table of Contents
Breitband-Radiometer
Breitbandradiometer ist die Bezeichnung für die Luxmeter und UV-Messgeräte die Reptilienhalter am häufigsten verwenden. Sie sind extrem einfach in der Anwendung, weil man sie nur unter die Lampe halten muss und den Messwert direkt am Display ablesen kann. Trotzdem lohnt sich ein genauerer Blick auf die Funktionsweise und Messfehler. Tatsächlich sind die Geräte oft tückischer als es auf den ersten Blick scheint.
Aufbau und Funktionsweise
Herz des Radiometers ist eine Photodiode. Dieser Halbleiterkristall erzeugt im Quasi-Kurzschluss-Betrieb elektrischen Strom, wenn er einfallendes Licht absorbiert. Der Strom wird verstärkt und ein Messwert, proportional zur Stromstärke, im Display angezeigt. Normalerweise wird Silizium als Halbleiter eingesetzt. Silizium ist empfindlich auf Strahlung zwischen 190 nm und 1100 nm mit einer maximalen Empfindlichkeit bei etwa 900 nm Wellenlänge. Durch verschiedene Filter kann die Empfindlichkeit des Halbleiters auf den gewünschten Bereich (z.B. UV) eingeschränkt werden. Daraus resultiert eine entscheidende systematische Fehlerquelle für Radiometer (⇒ Fehlerquelle spektrale Empfindlichkeit)
Anstelle einer Photodiode, die empfindlich im UV-Bereich ist, kann auch eine Photodiode für den sichtbaren Bereich zusammen mit einem Leuchtstoff, der UV-Strahlung in sichtbares Licht umwandelt verwendet werden. Ein solches Messgerät wurde in den 1950ern von Robertson in Australien entwickelt und von Berger in den USA modifiziert. Diese Variante ist meines Wissens nicht häufig im Einsatz.
Zusätzlich dient eine Streuscheibe der Kosinuskorektur
Effektive Bestrahlungsstärke
Ein Breitband-Radiometer weiß nichts über das Spektrum der Lichtquelle. Trotzdem hängt die Messung mit dem Spektrum zusammen. Das Breitbandradiometer misst immer eine effektive Bestrahlungsstärke. Die lässt sich auch aus dem mit dem Spektrometer gemessenen Spektrum berechnen. Weil das Breitband-Radiometer aber auf den “Zwischenschritt” der spektral aufgelösten Messung mit anschließender Integration verzichten, sind sie deutlich weniger empfindlich auf Rauschen.
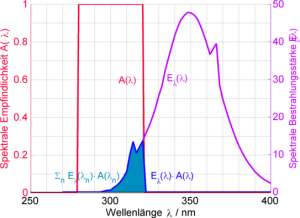
Aus der spektralen Messung erhält man die spektrale Bestrahlungsstärke $E_\lambda(\lambda)$ (z.B. in der Einheit µW/cm²/nm) für eine Reihe von Wellenlängen $\lambda$. Für jede dieser Wellenlängen wird die spektrale Bestrahlungsstärke $E_\lambda(\lambda)$ mit dem Wirkspektrum $W(\lambda)$ multipliziert. $W(\lambda)$ ist im Allgemeinen einheitenlos und hat einen Maximalwert von 1 oder 100%. Normalerweise liegen das Lampenspektrum $E_\lambda(\lambda)$ und das Wirkspektrum $W(\lambda)$ für unterschiedliche Wellenlängen vor. Die Wirkspektren sind oft in 1-nm-Schritten oder 5-nm-Schritten in der Literatur angegeben. Das Lampenspektrum wird vom Spektrometer in Schritten kleiner als 1 nm gemessen. Damit man die beiden Spektren für jede Wellenlänge miteinander multiplizieren kann, muss man das Wirkspektrum daher zuerst für die Wellenlängen des Lampenspektrums interpolieren.
Das resultierende Produktspektrum $E_\lambda(\lambda)\cdot W(\lambda)$ wird dann aufintegriert, so dass eine einzelne Zahl entsteht: $\int\mathrm{d}\lambda\,E_\lambda(\lambda)\cdot W(\lambda)$. Diese hat die Einheit µW/cm² (aus der Multiplikation von $E_\lambda(\lambda)$ und $\mathrm{d}\lambda$.
Manche effektive Bestrahlungsstärken werden anschließend noch mit einem Faktor multipliziert oder durch einen Divisor dividiert. So wird aus der effektiven Bestrahlungsstärke für Erythembildung, durch Division durch 2,5 µW/cm², der einheitenlose UV-Index. Die effektive Bestrahlungsstärke mit der Hellempfindlichkeitsfunktion des menschlichen Auges wird mit 6,83 lm/(µW/cm²)1) multipliziert, um die Beleuchtungsstärke in lx zu erhalten.
Es lohnt sich für das Verständnis und um ein Gefühl zu erhalten, diese Rechnung für verschiedene Lichtspektren und Wirkspektren selbst durchzuführen. Das “Thematic Network for Ultraviolett Measurements” hat eine frei zugängliche sehr lesenswerte Veröffentlichung zu UV-Radiometern (Characterizing the Performance of Integral Measuring UV-Meters 2000), die auch Lichtspektren enthält. Aus graphischen Darstellungen von Spektren lassen sich mit der kostenlosen Software engauge Zahlenwerte auslesen. Übungszwecken stelle ich Ihnen eine Excel-Datei zur Verfügung, mit der zwei Spektren $E_\lambda(\lambda)$ und $W(\lambda)$ multipliziert und integriert werden können.
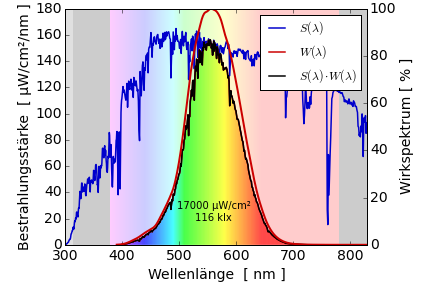
Effektive Bestrahlungsstärke (Berechnung von Lux) des Sonnenlichts
Um die Beleuchtungsstärke zu berechnen benötigt man als Wirkspektrum die Hellempfindlichkeitsfunktion des menschlichen Auges. Die Kurve hat ihr Maximum bei 555 nm Wellenlänge und fällt bis 400 nm und 700 nm Wellenlänge auf 0 ab.
Das Sonnenspektrum $E_\lambda(\lambda)$ wird an jeder Wellenlänge mit dem Wirkspektrum $W(\lambda)$ multipliziert. Da $W(\lambda=400\,\mathrm{nm})=0$ ist, ist auch das Produkt $E_\lambda(\lambda=400\,\mathrm{nm}) \cdot W(\lambda=400\,\mathrm{nm}) = 0$. Ebenso für $\lambda = 700\,\mathrm{nm}$. Das führt dazu, dass der blaue und der rote Anteil des Sonnenlichts kaum zur Beleuchtungsstärke beitragen.
Die effektive Bestrahlungsstärke ist das Integral $\int \mathrm{d} E_\lambda(\lambda) \cdot W(\lambda)$. Anschaulich ist das Integral die Fläche unter der Kurve $E_\lambda(\lambda)\cdot W\lambda)$. Man kann das Integral zur Kontrolle im Kopf nachrechnen: Die Form ist etwa dreieckig, mit einer Grundseite $g$, die von 400 nm bis 700 nm reicht, also 300 nm lang ist. Das Dreieck hat eine Höhe $h$ von 150 µW/cm²/nm. Die Fläche eines Dreiecks $F = \frac{1}{2}gh = \frac{1}{2}\cdot 300\,\mathrm{nm} \cdot 150\,\mathrm{µW/cm²/nm} = 22'500\,\mathrm{µW/cm²}$. Exakt gerechnet ist die Fläche etwas kleiner, weil $S(\lambda) \cdot W(\lambda)$ nicht exakt ein Dreieck ist, sondern an den Seiten “eingedrückt”.
Die 17'000 µW/cm² werden anschließend durch Multiplikation mit 6.83 lx(µW/cm²) in Lux umgerechnet: 116'000 lux.
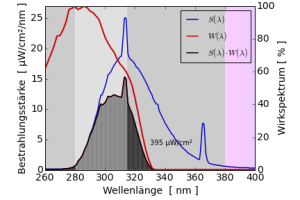
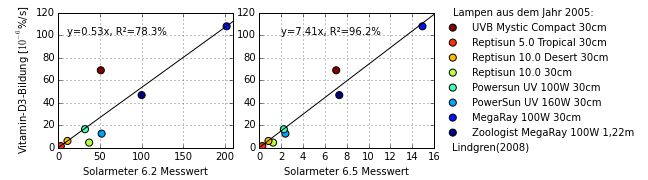
Solarmeter 6.2 Messwert zweier Leuchtstofflampen
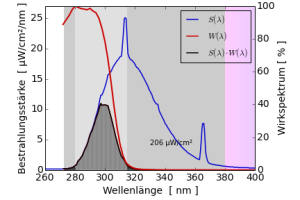
Das Solarmeter 6.2 $W(\lambda)$ hat eine maximale Empfindlichkeit bei einer Wellenlänge von 280 nm. Die beiden Spektren der UV-Lampen $E_\lambda(\lambda)$ haben ihre Maximum bei 340 nm und 313 nm Wellenlänge. Das Produktspektrum $E_\lambda(\lambda)\cdot W(\lambda)$ hat den höchsten Wert bei 310 nm. Die Wellenlänge, bei der das UVB-Radiometer seine maximale Empfindlichkeit hat (280 nm) trägt zum Messwert gar nicht bei, weil die spektrale Bestrahlungsstärke der beiden Lampen bei dieser Wellenlänge Null ist.
Da die beiden Lampen eine hohe spektrale Bestrahlungsstärke im Wellenlängenbereich zwischen 310 nm und 320 nm haben und das Wirkspektrum des UVB-Radiometers hier noch nicht auf Null abgefallen ist, ist es dieser Wellenlängenbereich der am stärksten zur effektiven Bestrahlungsstärke beiträgt. Allein aus dem Wirkspektrum des UVB-Radiometers wird das nicht sichtbar.
Obwohl es sich um ein UVB-Radiometer handelt, trägt auch der Bereich mit Wellenlängen größer als 320 nm zur effektiven Bestrahlungsstärke bei, die nicht zum UVB-Bereich gehören.
In diesem Beispiel sind die effektiven Bestrahlungsstärken 96 µW/cm² und 395 µW/cm², auch diese Zahlen lassen sich im Kopf mit der Dreiecksformel nachrechnen. Um den Messwert des Solarmeter 6.2 zu erhalten muss man diese Zahl noch mit einem Kalibrationsfaktor multiplizieren. Er wird hier ungefähr bei 1,53 liegen, d.h. für die beiden Lampen würde man Messwerte von ungefähr 147 µW/cm² und 604 µW/cm² erwarten.
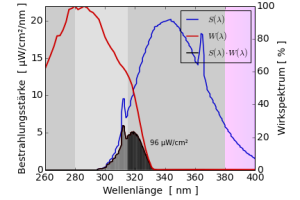
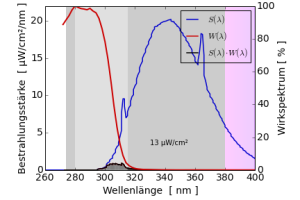
Solarmeter 6.5 Messwert zweier Leuchtstofflampen
Aus das Wirkspektrum des Solarmeter 6.5 $W(\lambda)$ hat eine maximale Empfindlichkeit bei einer Wellenlänge von 280 nm, fällt aber bereits bei einer Wellenlänge von 320 nm auf fast Null ab. Zusammen mit den beiden Lampenspektren trägt hier die Strahlung bei 300 nm bzw. 310 nm maximal zur effektiven Bestrahlungsstärke bei.
In diesem Beispiel sind die effektiven Bestrahlungsstärken 13 µW/cm² und 206 µW/cm², auch diese Zahlen lassen sich im Kopf mit der Dreiecksformel nachrechnen. Um den Messwert des Solarmeter 6.5 zu erhalten muss man diese Zahl noch mit einem Kalibrationsfaktor multiplizieren. Er wird hier ungefähr bei $\frac{0.32\mathrm{UVI}}{\mathrm{µW/cm²}}$ liegen, d.h. für die beiden Lampen würde man Messwerte von ungefähr UVI 4,1 und UVI 66 erwarten.
Fehlerquellen
Gegenüber Spektrometer haben Radiometer Vorteile: Sie sind leicht zu transportieren, leicht zu bedienen und zeigen nur eine einzige Zahl als Messwert an. Auch Reproduzierbarkeit der Messergebnisse, Auflösung und Signal-zu-Rausch-Verhältnis ist bei Radiometern ist oft besser als bei Spektrometern. Gerade für den UV-Bereich sind Radiometer robuster als Spektrometer (Webb 2000).
Radiometer haben aber natürlich auch Nachteile, die zu verschiedenen statistischen und systematischen Fehlern führen (Larason 2001). Luxmeter werden anhand dieser Messfehler beispielsweise in vier verschiedene Güteklassen einsortiert (DIN 5032 Teil 7). Die Güteklassen sind dann für verschieden Anwendungsgebiete geeignet.
Fehlerquelle: Spektrale Empfindlichkeit
Der größte Fehler bei Radiometern stammt aus der spektralen Empfindlichkeit des Messgeräts. Die verwendete Siliziumphotodiode misst jede Strahlung zwischen 190 nm und 1100 nm. Durch Filter muss der Bereich auf die gewünschten Wellenlängen eingegrenzt werden.
Wenn nur UVC-Strahlung gemessen werden soll, sind Filter nötig, die alle Strahlung mit einer Wellenlänge größer als 280 nm absorbieren. Diese Filter lassen aber gelegentlich doch Teile der UVA oder sichtbaren Strahlung durch. Wenn das UVC-Radiometer nur für Lichtquellen genutzt wird, die hauptsächlich UVC abstrahlen (z.B. UVC Desinfektionslampen) ist das unproblematisch. Nutzt man ein solches UVC-Radiometer aber für Sonnenlicht oder helle Terrarien-UV-Lampen kann das Messgerät „geblendet“ werden. Die Intensität der sichtbaren Strahlung und der UVA-Strahlung ist um viele Größenordnungen größer als die Intensität der UVC-Strahlung. Es kann passieren, dass das der Filter einen sehr kleinen Anteil der sichtbaren und UVA-Strahlung passieren lässt und dieser kleine Anteil immer noch viel intensiver als die UVC-Strahlung ist und das Messgerät daher einen fälschlicherweise zu großen Wert anzeigt. Im Fall der UVC-Strahlung kann man das teilweise überprüfen, in dem man einen UVC-Sperrfilter verwendet, der sichtbares Licht und UVA transmittiert aber UVC-Strahlung blockiert. Zeigt das UVC-Messgerät weiterhin einen Messwert an, ist bewiesen, dass der Messwert nicht durch UVC verursacht wurde. Diesen Effekt bezeichnet man auch als Out-of-Band-Response. Bereits dieser Out-of-Band-Response ist ein Beispiel für die Fehler, die sich aus der spektralen Empfindlichkeit des Messgeräts ergeben.
Out-of-Band-Responses habe ich praktisch bisher nur bei UVC-Messgeräten als relevant erlebt. Das folgende Beispiel gilt dagegen für alle Radiometer.
Wenn nur exakt der UVB-Bereich gemessen werden soll, müsste man Filter für die Siliziumphotodiode finden, die alle Strahlung mit der Wellenlänge größer als 315 nm und kleiner als 280 nm komplett absorbieren und alle Strahlung mit einer Wellenlänge zwischen 280 nm und 315 nm komplett ungefiltert durchlassen. Das ist nicht möglich. Stattdessen wird die spektrale Empfindlichkeit des Messgeräts immer eine glatte Kurve sein. Es wird nie ein UVB-Radiometer geben, das tatsächlich UVB misst. Tatsächlich misst das Messgerät etwas anderes, rechnet den Wert aber intern um und zeigt UVB in µW/cm² an. Das UVB-Radiometer wird so kalibriert, dass das der Messwert für eine Kalibrationslampe korrekt ist.
Diese Funktionsweise ist so ähnlich wie die Funktion von Messbechern für Mehl oder Zucker, die es in manchen Küchen gibt. Wenn man keine Waage hat, aber 300 g Mehl benötigt, schüttet man einfach so viel Mehl in den Messbecher bis die Marke für 300 g Mehl erreicht ist. Obwohl der Messbecher eigentlich etwas ganz Anderes misst (nämlich das Volumen des Mehls), kann man damit trotzdem die richtige Menge Mehl abmessen. Wenn man aber nun 300 g Zucker benötigt, dann funktioniert die Methode plötzlich nicht mehr. Das liegt daran, dass das Gewicht pro Volumen bei Mehl und Zucker völlig unterschiedlich ist. Das gleiche Problem entsteht, wenn man mit dem UVB-Radiometer die UVB-Strahlung einer Lampe messen will, die ein völlig anders Spektrum hat.
Misst man mit dem oben gezeigten UVB-Radiometer eine Lampe ohne UVB-Strahlung aber viel UVA-Strahlung, so wird das Messgerät einen Wert anzeigen, obwohl keine UVB-Strahlung vorhanden ist. Misst man eine Lampe mit UVB-Strahlung aber gänzlich ohne UVA-Strahlung, so wird der angezeigte Messwert zu klein sein: Das Messgerät “denkt” das auch UVA vorhanden wäre und korrigiert den Messwert nach unten.
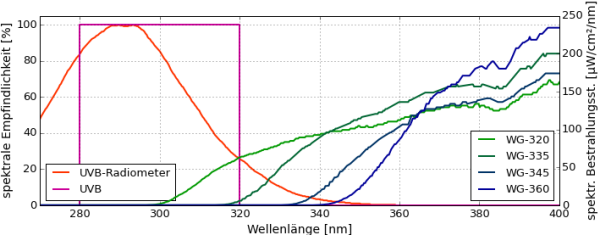
Dieser Fehler kann sehr dramatische Formen annehmen. Häufig zitiert wird im Terrarianerkreisen die Arbeit von Sayre & Kligman (Sayre & Kligman 1992). Sie verwendeten als UVB-Radiometer einen leider nicht näher spezifizierten Sensor von International Light mit maximaler Empfindlichkeit bei 290 nm. Als Lampe verwendeten sie eine Xenon-Kurzbogenlampe, deren Spektrum zusätzlich durch optische Langpassfilter verädert wurde. Ein WG-345-Filter lässt Strahlung mit einer Wellenlänge größer als 345 nm zu 90% passieren und absorbiert Strahlung mit einer Wellenlänge kleiner als 345 nm. Folgende Messwerte haben sie erhalten:
| Filter | UVB (290 - 320) spektral gemessen | UVB-Messwert Radiometer | relativer Fehler | Beurteilung |
|---|---|---|---|---|
| WG-320 | 600 µW/cm² | 38 µW/cm² | $\frac{600}{38}=\frac{16}{1}$, $\frac{38-600}{600}=-94\%$ | besorgniserregender Fehler, der einem Terrarianer im Vergleich zum Sonnenlicht aber aufgefallen wäre. |
| WG-335 | 12,4 µW/cm² | 12 µW/cm² | $\frac{12,4}{12}=\frac{1.03}{1}$, $\frac{12-12,4}{12}=-3\%$ | zufällig korrekter Wert, aber auch hier Wert sehr klein |
| WG-345 | 0,27 µW/cm² | 4.9 µW/cm² | $\frac{0,27}{4,9}=\frac{1}{18}$, $\frac{4,9-0,27}{0,27}=1700\%$ | kein relevanter Fehler, da Messwert korrekt nahe Null |
| WG-360 | 0,16 µW/cm² | 4.1 µW/cm² | $\frac{0,16}{4,1}=\frac{1}{25}$, $\frac{4,1-0,16}{0,16}=2460\%$ | kein relevanter Fehler, da Messwert korrekt nahe Null |
Manche lehnen UV-Radiometer in der Terraristik aufgrund dieser Fehler vollständig ab (Kober & Geissel 2015). Ich teile diese Ansicht nicht, aus mehreren Gründen:
- Die Fehler sind keinesfalls zufällig sondern lassen sich aus den Spektren und der spektralen Empfindlichkeitskurve erklären. Leider machen die Autoren keine näheren Angaben, welchen UVB-Sensor sie 1991 verwendet haben, ich verwende für die Erklärung daher einen der UVB-Sensoren, die 2015 auf der Webseite von IL abgebildet sind.
Die WG-360- und WG-345-Filter lassen so gut wie keine UVB-Strahlung durch. Das Spektrometer zeigt daher korrekt Werte < 0,3 µW/cm² an. Weil das UVB-Radiometer aber nicht nur UVB-Strahlung sondern auch UVA-Strahlung misst, zeigt es einen zu großen Wert an. Der WG-320-Filter lässt sehr wenig Strahlung unterhalb von 320 nm passieren, wovon die meiste Strahlung nahe an der Grenze zu 320 nm sitzt. Für ein Spektrometer zählt die Strahlung bei 319 nm bereits zu 100% als UVB-Strahlung. Das UVB-Radiometer zählt diese Strahlung nur zu 25%. Es ist daher verständlich, dass das Radiometer einen zu kleinen Wert anzeigt. - Der einzig wirklich besorgniserregende Fehler ist der Messwert mit WG-320-Filter: 38 µW/cm² anstelle von 600 µW/cm². So große Fehler kenne ich von anderen UVB-Radiometern nicht. Vielleicht war dieses Radiometer bereits alt und defekt, vielleicht war es auf besonders seltsame Weise kalibriert. Einem Terrarianer wäre das aber aufgefallen: Das Spektrum mit WG-320-Filter ist sehr ähnlich zum Sonnenspektrum in Südeuropa zur Mittagszeit. Dort erwartet man UVB-Messwerte größer als 400 µW/cm². Misst ein Terrarianer hier lediglich 38 µW/cm² wird er sicherlich skeptisch. Trotzdem sind UVB-Radiometer wegen der spektralen Empfindlichkeit insbesondere bei Terrarien-UV-Lampen mit wenig sonnenähnlichen Spektren sehr fehleranfällig und ich rate von ihrem Einsatz ab.
- Bei UV-Index-Radiometern tritt dieser Fehler aber auf. Allgemein ist der Fehler durch die spektrale Empfindlichkeit nur dann groß, wenn 1) die spektrale Empfindlichkeit des Radiometers schlecht zur Wunschkurve passt und 2) die Lampe viel Intensität im Bereich der schlechten Übereinstimmung hat.2) Der Fehler ist sehr viel kleiner, wenn die spektrale Empfindlichkeitskurve ähnlich zur gewünschten Messkurve ist. Die Empfindlichkeitsurve für Erythembildung, die Empfindlichkeitskurve für Vitamin-D-Bildung und die Hellempfindlichkeitskurve des menschlichen Auges sind glatte und wohl geformte Kurven, die man leicht mit Filtern nachbilden kann. Bei UV-Index-Messgeräten und Luxmetern tritt der Fehler daher kaum auf. Diese Messgeräte haben keinen systematischen Fehler von 1'700 % oder 2'460 %, wie bei Sayre & Kligman, sondern oft nur einen Fehler von 10 % oder in sehr ungünstigen Fällen von 30 % bis 50 % (siehe auch solarmeter).
Als UV-Radiometer sollten daher immer UV-Index-Radiometer verwendet werden, deren spektrale Empfindlichkeit sehr gut mit der tatsächlichen Funktion für den UV-Index übereinstimmt. Bei den Solarmeter 6.5 UV-Index-Radiometern ist das der Fall. Bei anderen Messgeräten muss die spektrale Empfindlichkeit beim Hersteller angefragt werden und kritisch geprüft werden. Wenn die spektrale Empfindlichkeit stimmt, halte ich den Einsatz von UV-Index-Radiometer in der Terraristik für sehr sinnvoll. Zur Sicherheit sollte man aber immer von einem möglichen Fehler von bis zu 30 % ausgehen und bei sehr exotischen Lampen doppelt vorsichtig zu sein.
Fehler f1'
Die Größe des Fehlers durch die Spektrale Empfindlichkeit wird mit dem Faktor $f_1'$ beschrieben.
\[ f_1' = \frac{ \int\mathrm{d}\lambda \left| W(\lambda)-K\cdot{}A(\lambda)\right| }{ \int\mathrm{d}W(\lambda) } \] dabei sind: $W(\lambda)$ gewünschte Wirkfunktion, die das Messgerät messen soll, $K\cdot{}A(\lambda)$ effektive Wirkfunktion inkl. Kalibration des Messgeräts. $f_1' = 0$, wenn die Spektrale Empfindlichkeit perfekt übereinstimmt ($W(\lambda)=K\cdot{}A(\lambda)$). Für den Fall das $W(\lambda)$ und $K\cdot{}A(\lambda)$ die gleiche Fläche haben aber keinen Überlapp wäre $f_1'=2$.
Für UV-Messgeräte schreibt DIN5031-11 vor f1 < 0,1 (Güteklasse 1), f1 < 0,2 (Güteklasse 2), f1 < 0,5 (Güteklasse 3) oder f1 < 1,0 (Güteklasse 4)
Für Luxmeter gilt nach DIN 5032-6 f1 < 0,015 (Güteklasse L), f1 < 0,03 (Güteklasse A), f1 < 0,06 (Güteklasse B) oder f1 < 0,09 (Güteklasse C)
Details zur Spektralen Empfindlichkeit
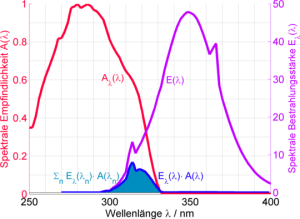
Als Formel ausgedrückt, ist das Stromsignal $S$ der Photodiode das Integral über das Produkt aus der spektrale Empfindlichkeit des Messgerätes ($A(\lambda)$, einheitenlos) und der spektralen Bestrahlungsstärke der Lichtquelle ($E_\lambda(\lambda)$, Einheit µW/cm²/nm): \[ S = \int\mathrm{d}\lambda E_\lambda(\lambda) = \Delta\lambda \cdot \sum_n E_\lambda (\lambda_n) \cdot A(\lambda_n) \] Diese Formel kann als Summe ($\sum_n$) oder als Integral ($\int$) geschrieben werden, und ist als Summe für mathematisch ungeübte Menschen wohl einfacher zu verstehen. Die Anweisung lautet: Bei jeder Wellenlänge $\lambda_n$ ($\lambda_n$ ist beispielsweise 280nm, 281nm, 282nm usw. in Schritten $\Delta\lambda=$1nm) wird die Bestrahlungsstärke des Lichts $E_\lambda(\lambda_n)$ gemessen und mit der spektralen Empfindlichkeit $A(\lambda_n)$ bei dieser Wellenlänge $\lambda_n$ multipliziert. Anschließend werden alle Werte addiert. Beispiel:
| $n$ | $\lambda_n$ | $E_\lambda(\lambda_n)$ | $A(\lambda_n)$ | $E_\lambda(\lambda_n)\cdot A(\lambda_n)$ |
|---|---|---|---|---|
| 1 | 280 nm | 0.002 µW/cm²/nm | 100 | 0.002 µW/cm²/nm |
| 2 | 285 nm | 0.001 µW/cm²/nm | 99 | 0.001 µW/cm²/nm |
| 3 | 290 nm | 0.035 µW/cm²/nm | 97 | 0.034 µW/cm²/nm |
| 4 | 295 nm | 0.049 µW/cm²/nm | 93 | 0.137 µW/cm²/nm |
| 5 | 300 nm | 0.529 µW/cm²/nm | 81 | 0.429 µW/cm²/nm |
| 6 | 305 nm | 1.829 µW/cm²/nm | 73 | 1.638 µW/cm²/nm |
| 7 | 310 nm | 5.477 µW/cm²/nm | 65 | 3.541 µW/cm²/nm |
| 8 | 315 nm | 13.442 µW/cm²/nm | 58 | 7.398 µW/cm²/nm |
| 9 | 320 nm | 13.627 µW/cm²/nm | 44 | 5.998 µW/cm²/nm |
| 10 | 325 nm | 17.569 µW/cm²/nm | 21 | 3.942 µW/cm²/nm |
| 11 | 330 nm | 25.637 µW/cm²/nm | 4 | 1.133 µW/cm²/nm |
| 12 | 335 nm | 32.354 µW/cm²/nm | 0 | 0.043 µW/cm²/nm |
| 13 | 340 nm | 41.639 µW/cm²/nm | 0 | 0.071 µW/cm²/nm |
| $\sum_n E_\lambda (\lambda_n) \cdot A(\lambda_n)$ | 24.36 µW/cm²/nm | |||
| $\Delta\lambda \cdot \sum_n E_\lambda (\lambda_n) \cdot A(\lambda_n)$ | 5 nm $\cdot$ 24.36 µW/cm²/nm = 121.8 µW/cm² | |||
Der Kalibrierungsfaktor wird so bestimmt, dass der Radiometer-Messwert für eine Kalibrierungslampe mit dem spektral ermittelten Messwert übereinstimmt. Dabei kann sowohl eine breitbandige Lichtquelle als auch ein Linienstrahler verwendet werden (Kärhä 2002). Als Linienstrahler wird üblicherweise eine Quecksilberdampflampe (254 nm, 313 nm, 365 nm) verwendet. Um den korrekten Messwert zu bestimmen, kann die Lampe mit einem einfachen Powermeter gemessen werden. Diese Methode ist schnell, einfach und sehr gut reproduzierbar. Bei Kalibration mit einer Linienlichtquelle liefert die Messung Bestrahlungsstärke einer breitbandingen Lichtquelle oft einen zu kleinen Wert, die Messung einer Linienlichtquelle einen zu hohen Wert (Gugg-Helminger, Dähn, & Fenk 2002). Für Anwendungen im medizinischen Bereich wird meist mit einer breitbandigen Lichtquelle kalibriert. Dazu muss die breitbandige Lichtquelle zusätzlich mit einem Spektrometer vermessen werden, um herauszufinden, welcher Wert der korrekte Messwert ist.
| UVB Messwert Spektrometer | $\int\mathrm{d}\lambda W(\lambda)E^\text{kalibr.}_\lambda(\lambda)$ | 140 µW/cm² |
|---|---|---|
| Stromsignal UV-Radiometer | $\int\mathrm{d}\lambda A(\lambda)E^\text{kalibr.}_\lambda(\lambda)$ | 122 µW/cm² |
| Kalibrierungs-Faktor | $K$ | 140/121.8 = 1.147 |
Der Messwert des Radiometer für eine Lichtquelle $E_\lambda(\lambda)$ ist letztlich \[ M = K\cdot \int\mathrm{d}\lambda A(\lambda)E_\lambda(\lambda) \]
Wenn das Spektrum der Kalibrierungslampe, die spektrale Empfindlichkeit des Messgeräts und das Spektrum der Lampe bekannt sind, kann man den entsprechenden Korrekturfaktor $a$ direkt berechnen (Gugg-Helminger, Dähn, & Fenk 2002).
\[ a = \frac{ \int\mathrm{d}\lambda E^\mathrm{kalibr.}_\lambda(\lambda)\cdot W(\lambda) }{ \int\mathrm{d}\lambda E^\mathrm{kalibr.}_\lambda(\lambda)\cdot A(\lambda) } \frac{ \int\mathrm{d}\lambda E_\lambda(\lambda)\cdot A(\lambda) }{ \int\mathrm{d}\lambda E_\lambda(\lambda)\cdot W(\lambda) } = \frac{ K \int\mathrm{d}\lambda E_\lambda(\lambda)\cdot A(\lambda) }{ \int\mathrm{d}\lambda E_\lambda(\lambda)\cdot W(\lambda) } \]
Man kann sogar einen Schritt weiter gehen und einen Korrekturfaktor für diese Lampe und dieses Radiometer für ein anderes Wirkspektrum berechnen. Sobald man diesen Korrekturfaktor hat, kann man ein UVB-Radiometer theoretisch auch verwenden um (für diese spezielle Lampe!) den UV-Index oder die effektive Bestrahlungsstärke für Vitamin D zu messen.
Beispiel:
| Breitbandmessgerät | Spektrometer | Korrekturfaktor | |
|---|---|---|---|
| UVB: | 89,6 µW/cm² | 98 µW/cm² | 98/89,6 = 1,09 |
| Vitamin D: | - | 14 µW/cm² | 14/89,6 = 0,156 |
| Breitband-Messwert | korrigiert für UVB ( x 1,09) | korrigiert für Vitamin D ( x 0,156 ) |
|---|---|---|
| 50 µW/cm² | 54,5 µW/cm² | 7,8 µW/cm² |
| 100 µW/cm² | 109 µW/cm² | 15,6 µW/cm² |
| 150 µW/cm² | 163,5 µW/cm² | 23,4 µW/cm² |
| 200 µW/cm² | 218 µW/cm² | 31,2 µW/cm² |
| 300 µW/cm² | 327 µW/cm² | 46,8 µW/cm² |
Der Korrekturfaktur muss für jedes Messgerät ($A(\lambda)$ mit Kalibrierung $K$) und jede gewünschte Anwendung (Wirkungsspektrum $W(\lambda)$ und Lampe $E_\lambda(\lambda)$) bestimmt werden. Will man die Abhängigkeit von der konkreten Lampe reduzieren, bietet sich, der “Integral characterisation factor” $f_1'$ an (Characterizing the Performance of Integral Measuring UV-Meters 2000) 3) : \[ f_1' = \frac{ \int\mathrm{d}\lambda \left| W(\lambda)-K A(\lambda)\right| }{ \int\mathrm{d}W(\lambda) } \]
Übersicht über einige Korrekturfaktoren, siehe auch (Hoffmann & Kirschner 2010)
| Quelle | Lichtquelle | Messbereich | Abweichung Breitband/Spektrometer | spektraler Korrekturfaktor | |
|---|---|---|---|---|---|
| 121 | Xenon+Filter | UV-Index | 1/1.85 - 2.22 | verschiedene Handelsübliche UV-Messgeräte | |
| 121 | Xenon+Filter | dUVA | 1/1.3 - 5.51 | verschiedene Handelsübliche UV-Messgeräte | |
| 320 | VitaminD-Bildung | ||||
| 474 | VitaminD-Bildung | ||||
| 38 | UV-Lampen | UV-Index | 1/2-5 - 1.6 | ||
| 38 | Sonne | UV-Index | 1.2 - 2.2 | ||
| 277;667 | Xenon+Filter | UVA | 1.18 - 1.42 | ||
| 277;667 | Xenon+Filter | UVB | 1/25 - 16 | ||
| 676 | Sonne (132 Spektren) | UV-Index | R²=99.8% | ohne Korrekturfaktoren | |
| 676 | Sonne (132 Spektren) | UV-Index | R²= 99.98% | nach Korrektur für SZA und Ozon | |
| 119 | UV-Lampen,Sonne | UV-Index | 0.7-6.3 | ||
| Conrad | Glühlampen/Tageslicht | Lux | 1,000 | ||
| Conrad | tageslichtweiße LEDs | Lux | 0,990 | ||
| Conrad | Neonröhren weiß | Lux | 0,870 | ||
| Conrad | Neonröhren blau | Lux | 1,286 | ||
| Conrad | Neonröhre grün | Lux | 1,167 | ||
| Conrad | Neonröhre rot | Lux | 0,671 |
Fehlerquelle: Kosinuskorrektur
Ein wichtiger Fehlerbeitrag ist die Kosinuskorrektur des Radiometers (siehe detaillierter auch Abschnitt Kosinuskorrektur unter Spektrometer). Wenn Licht schräg auf eine Fläche scheint, verringert sich die Intensität der Strahlung auf der Oberfläche. Messgeräte reagieren nicht immer korrekt auf Licht aus verschiedenen Winkeln. Eine entsprechend dimensionierte Streuscheibe mit Abschattungsringen kann das korrigieren.
Fehlerquelle: Temperaturabhängigkeit
Sowohl die spektrale als auch die absolute Empfindlichkeit des Radiometers kann temperaturabhängig sein, so dass ein Messgerät, das durch die Wärmestrahlung der Lampe aufgeheizt wird, veränderte Werte liefert. Beim einem Solarmeter 6.2 wurde eine sehr geringe Erhöhung der Messwerte bei Temperaturen größer als 40°C ermittelt (Baines 2007).
Fehlerquelle: inhomogene Lichtverteilung
Bei Messgeräten mit einem großen Eingang, kann eine inhomogene Lichtverteilung über die Sensorfläche und das Gesichtsfeld des Sensors den Messwert verfälschen ((Harrison 2000),(Larason 2001)).
Fehlerquelle: Flackern (Modulation)
Auch eine Modulation der Lichtintensität, z.B. bei stark flackernden Mischlichtlampen kann falsche Messwerte erzeugen.
Fehlerquelle: Dunkelsignal
Insbesondere wenn sehr kleine Messwerte gemessen werden sollen, spielt das statistische Dunkelsignal der Photodiode eine Rolle. Das Rauschen von Radiometern ist aber - vor allem im Vergleich zu günstigen Spektrometern - sehr gering.
Fehlerquelle: Alterung
Durch den Einfluss der UV-Strahlung können UV-Radiometer altern. Es ist empfehlenswert, regelmäßig eine Vergleichsmessung mit einer Lichtquelle bekannter UV-Strahlung oder mit einem wenig genutzten UV-Radiometer durchzuführen.
Fehlerquelle: Linearität
Photodioden zeichnen sich normalerweise durch eine hohe Linearität aus, d.h. bei doppelter Bestrahlungsstärke zeigt das Radiometer auch tatsächlich den doppelten Wert an. Es gibt jedoch auch defekte Messgeräte, bei denen das nicht mehr der Fall ist. In (Christiaens & Chardon 2006) wurde ein älteres UVB-Radiometer gefunden, das bei hohen Bestrahlungsstärken einen um den Faktor 4 zu großen Messwert anzeigte. Dieser Fall ist selten, aber man sollte wissen, dass das möglich ist.
Literatur
763;119;676;38;277;667;474;320






Discussion